00-1010拉格朗日中值定理说，如果函数f(x)在闭区间[a，b]中是连续的，在开区间(a，b)中是可导的，那么在(a，b)中至少有一点，所以

或者

拉格朗日中值定理意味着：

画一条线连接图像中的两点A和B。要求所画直线的每个点都是连续可导的。那么你画的直线中至少有一点的切线与连接A和b的直线平行。

我们可以用一个直观的例子来说明这个中值定理的含义：

有一辆车在加速，从0到200米的距离前进需要8秒。很容易计算出汽车在这8秒钟内的平均速度是25米/秒，所以汽车的速度在这8秒钟内的某个时刻必须正好是25米/秒。

接下来，柯西说他有话要说：

00-1010柯西中值定理说，如果函数f(x)和F(x)在闭区间[a，b]中是连续的，在开区间(a，b)中是可导的，并且对于任意x(a，b)存在F'(x)0，那么在

这篇文章可能不容易理解，但让我们改变一下，看看你是否熟悉它：

这不就是刚才拉格朗日中值定理的别墅二层楼的形式吗，这里就不多解释了。

柯西中值定理是拉格朗日中值定理的推广，是微分学的基本定理之一。几何意义是由参数方程表示的曲线上至少有一点，其切线与两个端点所在的弦平行。这个定理可以看作是参数方程下拉格朗日中值定理的表达。

柯西中值定理大致表明，对于给定的两个端点之间的平面圆弧，至少有一个点，圆弧的切线通过其端点与切线平行。

00-1010在柯西中值定理中，如果g(x)=x，其结论形式与拉格朗日中值定理相同。

因此，拉格朗日中值定理是柯西中值定理的特例。相反，柯西中值定理可以看作是拉格朗日中值定理的推广。

拉格朗日中值定理：

00-1010如果u=f (x)和v=g (x)，这种形式可以理解为参数方程，而f(b)-f(a)/g(b)-g(a)是连接参数曲线两端的弦的斜率，f' ()/g' (

由参数方程表示的曲线上至少有一点，该点的切线与连接两个端点的弦平行。

柯西中值定理：

10-1010柯西中值定理是用拉格朗日余数证明n阶bhdlq公式最重要的应用，只要多次重复使用柯西中值定理就可以证明。下面是n=1的一个例子。

例1

设f(x)在(a，b)中是两次可微的，证明了任意x，x0(a，b)在x和x0之间存在，这样

这是函数f(x)在点x0附近的一阶bhdlq公式。

证明：订单

"https://p26.toutiaoimg.com/origin/pgc-image/d2bf5f97549045e8a171beb3fb8ce82a?from=pc">

G(x)=(x-x0)²利用

在两次应用到柯西中值定理后可以得到：

命题得证。

2.洛必达法则

柯西中值定理的一个最重要的应用就是可以推导计算待定型的极限最有效的方法——洛必达法则。

洛必达法则是求两个无穷小量或两个无穷大量的比的极限。在满足一定条件下可以化成两个函数的导数的比值极限，这样就有可能使得原待定型变成简便而有效的求非待定型极限的问题。

我们得出下面这个定理（洛必达法则）：

⑴ 两个函数f(x)和g(x)在开区间(a,b)可微，并且在这个开区间上，g(x)的导数不等于0；

⑵ 存在极限

其中A为一个有限的常数。则在以下情况下：

或者

那么就有：

在区间的另一个端点也存在相类似的结果。这个定理就称之为洛必达法则，能有效地应用于待定型的极限计算。

3.不等式

柯西中值定理在不等式的证明也有广泛应用，关键是f(x)和g(x)要选得恰当。

例2

试证明当x>0时，1+x ln(x+√1+x²)>√1+x²。

证明：设

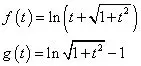
则f(t)和g(t)在区间[0,x]上满足柯西中值定理条件，所以存在ξ∈(0,x)，使

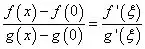
即

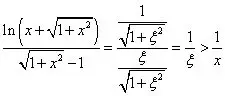
结论得证。

4.中值点

中值点的存在性的证明是柯西中值定理最典型的应用之一。

例3

设a>0，函数f(x)在区间[a,b]上连续，在(a,b)内可导，则存在ξ∈(a,b)，使得

证明：设F(x)=f(x)/x，G(x)=1/x，显然F(x),G(x)在[a,b]上满足柯西中值定理的条件，于是存在ξ∈(a,b)，使得

即存在ξ∈(a,b)，使得

即可得结论。

怎么样你学会了吗？动动手指转发给更多的同学吧！